Eureka 2012 | Level B – Problems and Solutions
Level B Grades 9-10
- 1. A person made a purchase for D dollars and C cents, and gave the cashier a $20 bill. The cashier incorrectly charged the person C dollars and D cents, and returned $4.88 in change. If the cashier had charged the correct price, what would the correct change have been?
Correct answer: $7.85
Solution:
20 – 4.88 = 15.12. Switch the dollars and cents to get 12.15. 20 – 12.15 = 7.85
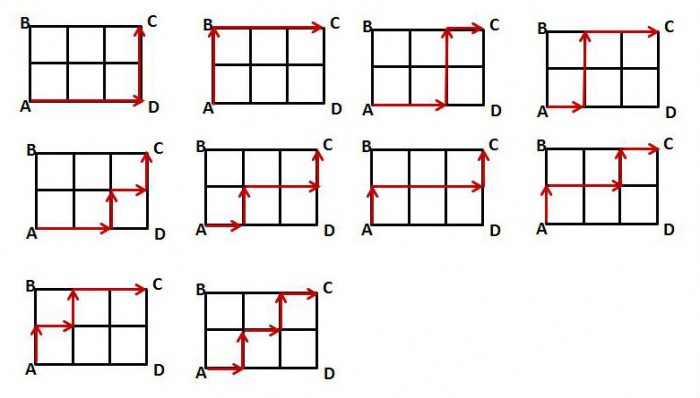
- 2. ABCD is a rectangle whose sides are 3 units and 2 units long. The length of the shortest path from A to C following the lines of the diagram is 5 units. How many different shortest paths are there from A to C?
- 3. A printer has to number the pages of a book from 1 to 150. Suppose the printer uses a separate piece of type for each digit in each number. How many pieces of type will the printer have to use?
Correct Answer: 342
Solution:
Pages: Pieces of Type:
1 – 9 9 x 1 = 9
10 – 99 90 x 2 = 180
100 – 150 51 x 3 = 153
Total: 342
- 4. What is larger 1/1001 + 1/1002 + 1/1003 + 1/1004 + ….+1/3001 or 1? Explain your answer.
Correct answer: The left side is larger than 1.
Solution:
Use inequality (see proof below) as follows: 1/a + 1/b ≥ 2 / average (a,b).
If we apply this inequality 1000 times we get:
1/1000 + 1/3000 ≥ 2/2000
1/1001 + 1/2999 ≥ 2/2000
…..
1/1999 + 1/2001 ≥ 2/2000
If you sum all of these 1000 inequalities, you will get that the overall sum is larger than 1.
Proof of original inequality…. It follows from a2 + b2 ≥ 2ab. => (a+b)2 ≥ 4ab =>
(a+b)/ab ≥ 4 /(a+b) => 1/a + 1/b ≥ 2 / average(a,b)
- 5. Farmer bought 100 farm animals for $1000. Cows were $100 each, sheep $30 each, and piglets $5 each. How many of each kind did he buy?
Two possible correct answers:
(5 cows, 1 sheep, 94 piglets) or (0 cows, 20 sheep, 80 piglets).
Solution:
C= cows, S = sheep, P = piglets. All non-negative integers. C + S + P = 100 and 100C + 30S + 5P = 1000. Simplify the second equation by dividing it 5. 20C + 6S + P = 200. Subtract the first equation from the 2nd one. The result is 19C + 5S = 100. We can now deduce that C must be divisible by 5, since 5S = 100 – 19C. There are only 3 choices for C then: 0, 5, and 10. Let’s plug them in and see… C=10 is not an option. If C = 5, then S = 1, because 19C + 5S = 100. Then P = 94. If C=0, S=20. Then P= 100 – S – P = 80. Two possible correct answers: (5,1, 94) and (0,20,80).
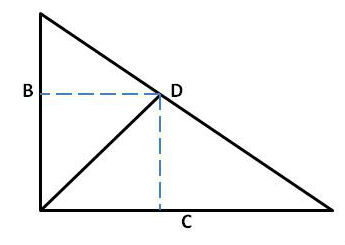
- 6. Legs of a right triangle are B and C. Find length of the right angle bisector.
Let the bisector cross the hypotenuse at point D. Let’s draw perpendicular lines from D to legs B and C. They form a square with a side X. It easily follows that X /C = (B – X) / B. Therefore, X = BC / (B+C). The bisector is equal to X*√(2), because the bisector is the diagonal of the square. Therefore, the bisector is BC / (B+C) * √(2). General solutions that use formula for bisector as a function of sides of a triangle are acceptable as well.
- 7. Beauty and the Beast are playing a game. They are taking turns at breaking a chocolate bar, 6×9 squares, along the straight lines. Whoever can’t break the chocolate any further loses the game. Beauty started first. Who is going to win the game? How many turns will they take before the game is over?
Correct Answer: Beauty will win after 53 turns
Solution:
The game starts with exactly 1 piece of Chocolate. They must break it along straight lines. Key Observation: upon each move, a piece of chocolate is broken into 2, so the total number of pieces of chocolate increases by 1 at each turn. At the end of the game there will be 54 single squares of chocolate. Therefore, it will take 53 turns before the game is over (regardless of how they play it). Since Beauty took the 1st turn, she will also take the 53rd one. Beauty will win.
- 8. Athos, Porthos, Aramis, and d’Artagnan were playing Tug of War. Athos and Porthos easily beat Aramis and d’Artagnan. Porthos and d’Artagnan just barely beat Aramis and Athos. Finally, Porthos and Aramis were tied for a victory with Athos and d’Artagnan. Please rank all 4 musketeers by strength from strongest to weakest.
Correct Answer: (From strongest to weakest) Porthos, Athos, d’Artagnan, Aramis.
Solution:
A = Athos, P = Porthos, R = Aramis, and D = d’Artagnan.
What do we know?
A + P >> R +D, P + D >≈ R + A, and P + R = A + D
These are the only 3 ways in which 4 musketeers can be split into 2 teams of 2. Porthos is clearly the strongest, because he never lost. Aramis (R) is the weakest, because he never won. Since the strength of the Porthos’s team became lower after we swapped A and D, we can conclude that A >D. Therefore, P>A>D>R.
- 9. Prove that ∛(20+14√2) + ∛(20-14√2) = 4
Solution:
(a+b)3 = a3 + 3a2b + 3ab2 + b3
Therefore:
(2+√2)3 = 8 + 12√2 + 12 + 2√2
(2-√2)3 = 8 – 12√2 + 12 – 2√2
20 + 14√2 = (2 + √2)3; 20 – 14√2 = (2 – √2 )3
The identity above follows easily, since (2+√2) + (2-√2) =4
- 10. A team of farmers has to plow two fields; one field is twice as large as the other one. After ½ day of work on the larger field, the team has split: ½ of the team stayed on the larger field, and finished it by the end of the day. The other ½ of the team that went to the smaller field couldn’t finish it by the end of the day. Next day one farmer finished plowing the rest of the smaller field with a full day of work. How many farmers are in the team?
Correct answer: 8 farmers.
Solution:
Let X = area that one farmer can plow in a day. Let N = number of people in a team. How big was the 1st field? Half the team worked there for the whole day, and half the team worked for ½ day. So the size of the 1st field is NX/2 + NX/4 = 3NX/4. How big is the second field? Half the team worked there for ½ day, and one person worked for a full day. So the size of the 2nd field is NX/4 + X. We also know that 1st field is twice as large. Therefore,
3NX/4 = 2 * (NX/4 + X). If we cancel X on both sides we get 3N/4 = 2 * (N/4 + 1). This solves to N = 8.